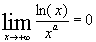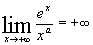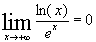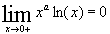La fonction Exponentielle

• 1) Définition et Propriétés

 

Définition : la fonction exponentielle est la fonction réciproque du logarithme népérien ln.

Exp=(ln)^-1 définie comme suit :

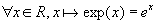
De plus, si y=e^x ó x=ln(y) et y Î R*₊

Propriétés : " a, bÎ R,

• e^a+b=e^a*e^b
• e^a-b=e^a/e^b
• e^-a=1/e^a
• e^ab=(e^a)^b

e^x est continue, dérivable sur R et de dérivée : (e^x)'=e^x

De plus, si y=e^x ó x=ln(y) et y Î R*₊

Propriétés : " a, bÎ R,

• e^a+b=e^a*e^b
• e^a-b=e^a/e^b
• e^-a=1/e^a
• e^ab=(e^a)^b

e^x est continue, dérivable sur R et de dérivée : (e^x)'=e^x

 

• 2) Etude de la fonction

 

Limites :

• 
• 
• 
• 
• 

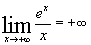
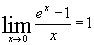
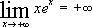
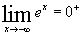
Tableau de Variations :

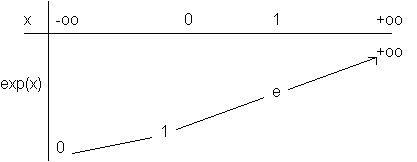
Courbe :

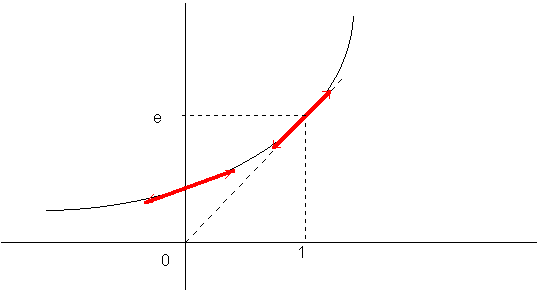
La primitive de e^x sur R est e^x. e^x est continue, strictement croissante de R sur R^*+, e^x est donc une bijection de R sur R^*₊.

 

• 3) Fonctions Puissances

 

Définition : Soit aÎ R, xÎ R^*₊ alors la fonction x^a=e^aln(x) est continue, dérivable sur R^*₊ de dérivée : (x^a)'=ax^a-1.

Croissances Comparées : a>0

• 
• 
• 
• 
•