Derivées et calcul différentiel
- 1) DEFINITIONS et PREMIERE APPROCHE
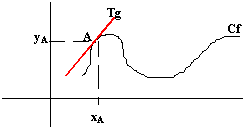
Definition: On appelle nombre dérivé d'une fonction f(x) en un point A(xA ; yA), le coefficient directeur de la tangente à la courbe Cf au point A.(cf dessin)
Ce nombre, s'il éxiste, peut être calculé grâce aux deux formules suivantes :
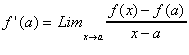
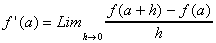
A SAVOIR : Si la limite n'existe pas (+inf, -inf), alors, la fonction n'est pas dérivable au point considéré.
Exemple : soit f(x)=2x-3. Calculer f'(4)
solution :
(que l'on retrouve avec les formules).
NB : On a donc l'équation de la tangente en un point A : y=f'(a)(x-a)+f(a)
Définition : Une fonction f(x) est d érivable sur un intervalle I ssi elle est dérivable en tout point de I.
NB : En fait le domaine de dérivabilité de f(x) correspond au domaine de définition de sa fonction dérivée.
- 2) DERIVEES DES FONCTIONS USUELLES ET OPERATIONS
Dérivées à connaître et formules utiles
fonctions : f(x) dérivées f'(x) aR 0 x 1 ax a xn, nR nxn-1 1/x -1/x2 x 1/2x ln(x) 1/x ex ex sin(x) cos(x) tan(x) 1+tan2(x) ou 1/cos2(x) cos(x) -sin(x) u(x)n nu'(x)u(x)n-1 u(x) u'(x)/2u(x) ln(u) u'(x)/u(x) eu(x) u'(x)eu(x) Une astuce : Une seule formule très importante à retenir : un=nu'un-1. En effet, pour u on pose n=1/2, et pour 1/u, on pose n=-1. Avec u une fonction quelle qu'elle soit. De même 1/ua avec n=-a. Essayez donc ! ! !
Formules de Composition et d'opérations de Fonctions :
(u+v)'=u'+v'
(uv)'=u'v+v'u
(u/v)'=(u'v-v'u)/v2
[u(v(x))]'=v'u'(v(x))