Denombrements - Probabilité

• 1) Théorie des ensembles

 

Cardinal : l e cardinal d'un ensemble E noté card(E) est le nombre d'éléments de cet ensemble.

Propriété : card(AUB)=card(A)+card(B)-card(AB)

Cas particulier : si AB=0 (A et B disjoints) alors card(AUB)=card(A)+card(B)

Complémentaire : Le complémentaire d'une partie A d'un ensemble E notée C_EA= représente les éléments de E qui ne sont pas dans A :

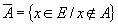
Propriétés :

• AU=E
• A=0
• Card(E)=card(A)+card()

Produit Cartésien : le produit cartésien de deux ensembles E et F, noté ExF le couple (x,y) tel que x est un élément de E et y un élément de F:

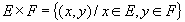
On a : card(ExF)=card(E)*card(F)

Propriété : Soit E un ensemble tel que card(E)=n, alors le nombre de p-uplets de E est n^p

Arrangements : Les arrangements de p éléments de E sont les p-uplets de E constitués d'éléments distincts, si p>n, avec n=card(E), alors il n'existe pas d'arrangement possible.

On a alors :

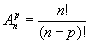
Combinaisons : On appelle combinaison de p éléments de E tout sous ensemble de E possédant p éléments de E et on note :

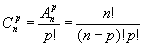
Propriétés :

• 
• 
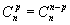
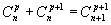
• (a+b)ⁿ=

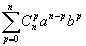
Définition : L'ensemble des parties d'un ensemble E noté P(E) est tel que : cardP(E)=2ⁿ (card(E)=n)

 

• 2) Probabilités

 

Comparaison théorie des ensembles Probabilité

Langage ensembliste	Langage probabiliste
Ensemble des résultats	Univers
1 élément de cet ensemble ou sous-ensemble ou partie de l'ensemble des résultats	1 événement élémentaire
AUB	A ou B
AnB	A et B
CEA	Evénement contraire de A :
Ensemble disjoints	A et B incompatibles

Définition : Une probabilité sur U c'est associer chaque événement élémentaire un nombre réel positif pi (proba de l'événement élémentaire ai). La suite des nombres pi devant vérifier :

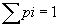
Propriétés :

• P(A)=card(A)/card(U)
• P(AUB)=P(A)+P(B)-P(AnB)
• P(AUB)=P(A)+P(B) si A et B sont incompatibles
• P()=1-P(A)

Méthode avec les dénombrements :

Beaucoup de problèmes peuvent se ramener à l'étude des différentes façons de tirer p boules dans une urne qui en contient n.

Type de tirage	Ordre	Répétition d'élets	Dénombrement
Successif avec remise	On tient compte de l'ordre	Un élt peut être tiré plusieurs fois	np-uplets
Successif sans remise		Un élt n'est tiré qu'une seule fois	Anp
Simultanée	L'ordre n'intervient pas		Cnp

RQ : Les arrangements de n élts de E sont appelés Permutation de E : A_nⁿ=n!, c'est n! façons d'ordonner une liste de n éléments