Courbes paramétrées

• 1) Définitions

 

Définitions :

• Soient f et d définies sur un même intervalle I, soit C={M(x,y)} la courbe telle que : x=f(t) et y=g(t) avec t un élément de I
• C est appelée courbe paramétrée dont une représentation paramétrique est :

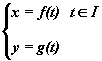
Théorème   : Soit C : , t₀ de I, si f et g sont dérivables en t₀, on pose : , si , c'est un vecteur directeur de la tangente à la courbe en M_t0 (point de paramètre t₀)

Equation de la tangente :

 

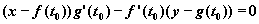
• 2) Etudes

 

Propriétés  :

• Si f et g sont périodiques de période T, alors M(t+T)=M(t), on étudie la courbe sur un intervalle d'amplitude T.
• Si f et g sont paires, M(-t)=M(t) on étudie la courbe sur InR₊ (les éléments positifs de I).
• Si f et g sont impaires, M(-t)=-M(t), symétrie par rapport à O(0,0), on étudie la courbe sur InR₊, et on effectue une symétrie par rapport à O(0,0).
• Si f est paire, g impaire : M(-t)=(f(t) ;-g(t)) ; symétrie par rapport à l'axe Ox.
• Si f impaire et g paire : M(-t)=(-f(t) ;g(t)) ; symétrie par rapport à l'axe Oy.

• 3) Exemples

 

avec et R>0 : cercle de centre O de rayon R.

 : Courbe y=f(x)

 : Droite passant par M₀(x₀ ;y₀) de vecteur directeur

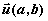
 : Parabole de paramètre p.

 : Hyperbole avec t non nul.

 : avec , Ellipse.