Continuité - études de fonctions

• 1) Continuité

 

Définition : f est continue en un point a si et seulement si

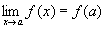
Propriétés : Soit f et g deux fonctions continues en un point a, alors :

• |f| est continue en a
• kf est continue en a avec k réel
• 1/f continue en a si f(a)
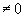
• (f+g) continue en a
• fg continue en a
• gof continue en a

Continuité sur un intervalle : f est continue sur un intervalle I si et scellement si elle est continue en tout point de I.

Théorème : Soi t f définie sur I et a, alors si f est dérivable en a, elle est continue en a .

ATTENTION : LA RECIPROQUE EST FAUSSE ex : f(x)=|x| pas dérivable en 0.

Prolongement par continuité : Soit f non définie en a et la fonction g définie par: est continue en a et s'appelle le prolongement de f par continuité en a.

RQ : Une fonction f composée de foncti ons continues est elle-même continue!!!(très utile)

 

• 2) Etude de fonctions

 

Méthode :

• Trouver le domaine de définition de la fonction
• Regarder la périodicité (éventuelle) de la fonction (réduction du domaine d'étude à une période).
• Parité de la fonction (symétries)
• Domaine d'étude
• Dérivabilité, domaine et calcul de la dérivée.
• Signe de la dérivée.
• Tableau de Variations
• Limites aux bornes et aux points non définis
• Calcul d'asymptotes
• Dessin de la courbe (ne pas oublier les tangentes )