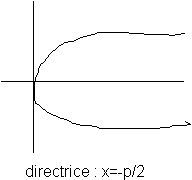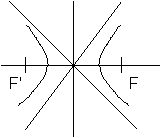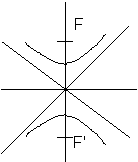Les Coniques

• 1) Définitions

 

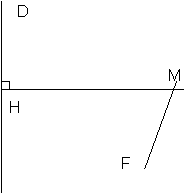
Définition : Soit D une droite, F un point du plan tel queF n'appartient pas à D. On appelle Conique de foyer F, de direction D et d'extrémité e l'ensemble : avec H projeté orthogonal de M sur D.

Types de Coniques suivant les valeurs de e :

• e>1 hyperbole
• e=1 parabole
• 0<e<1 ellipse

Définitions :

• Axe focal : droite passant par F et perpendiculaire à la directrice. L'axe focal est un axe de symétrie.
• Sommet : On app elle sommet d'une conique les points de cette conique appartenant à l'axe focal.

• 2) Equations réduites

 

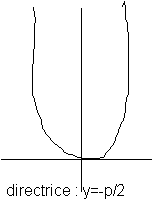
La Parabole :

Equation dans le repère (S,i,j) avec S sommet de la parabole, i de même sens que et j vecteur directeur de la directrice. On posera p=d(F,D) et F(p/2; 0).

L'équation de la directrice est alors : s=-p/2.

Les indications ci dessous sont valables pour p<0 et p>0.

Equation	Y2=2PX	X2=2PY
Sommet	Centre du nouveau repère	Idem
Axe focal	Nouvel axe des abscisses	Nouvel axe des ordonnées
Foyer	F(p/2;0) dans nouveau repère	F(0;p/2) dans nouveau repère
Dessin

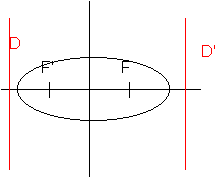
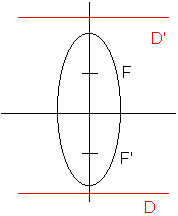
Ellipse

L'équation est du type : avec . e=c/a et b=Ö (a²-c²) d'où c=Ö (a²-b²)

Deux foyers : F et F'. Deux directrices D, D'.

C'est une conique à centre.

Théorème : Les coniques à centre admettent 2 paires de directrices et foyers symétriques par rapport au centre.

	a>b	a<b
Centre	Centre du nouveau repère	Idem
Axe focal ou Grand Axe	Axe des abscisses du nouveau repère (y=0)	Axe des ordonnées du nouveau repère (x=0)
Sommets dans nouveau repère	A(a,0); A'(-a,0) sur l'axe focal et B(0,b) et B'(0,-b) sur l'autre axe	B(0,b) et B'(0,-b) sur l'axe focal et A(a,0); A'(-a,0) sur l'autre axe
Foyers dans nouveau repère	F(c,0) et F'(-c,0) tel que c=Ö (a2-b2)	F(0,c) et F'(0,-c) tel que c=Ö (b2-a2)
Directrice	X=a2/c et X=-a2/c	Y=b2/c et Y=-b2/c
Excentricité	e=c/a	e=c/b
Dessin

L'Hyperbole

L'équation de l'hyperbole est et a,b,c et e ont les mêmes propriétés que pour l'ellipse.

Equation dans nouveau repère
Centre	Centre du nouveau repère	Idem
Axe focal ou Grand Axe	Axe des abscisses du nouveau repère (y=0)	Axe des ordonnées du nouveau repère (x=0)
Sommets dans nouveau repère	A(a,0); A'(-a,0)	B(0,b) et B'(0,-b)
Foyers dans nouveau repère	F(c,0) et F'(-c,0) tel que c=Ö (a2-b2)	F(0,c) et F'(0,-c) tel que c=Ö (b2-a2)
Directrice	X=a2/c et X=-a2/c	Y=b2/c et Y=-b2/c
Asymptotes	Y=(b/a)x et y=-(b/a)x	Y=(b/a)x et y=-(b/a)x
Excentricité	e=c/a	e=c/b
Dessin