Nombre Complexe
- 1) Définitions et Opérations
- Un complexe est un nombre z noté z=a+ib où a et b sont des réels. On appelle C l'ensemble des complexes tel que C={a+ib, (a,b) Î R´ R}. On prendra i tel que i2= - 1.
- La partie réelle de z Ré(z)=a et la partie imaginaire de z est Im(z)=b.
- z1+z2=(a1+a2) + i(b1+b2)
- z1z2=(a1a2-b1b2)
+ i(a1b2+a2b1)
- z1=z2Û a1=a2 et b1=b2
- 2) Conjugaison et Module
Définitions :
Opérations :
Conjugaison :Soit z=a+ib, on appelle zbar le complexe conjugué de z.
zbar=a-ib.
- z+zbar=2a zzbar=a2+b2z-zbar=2ib (zbar)bar=z si z¹ 0 : (1/z)bar=1/zbar
- (z1z2)bar=z1bar*z2bar(z1+z2)bar=z1bar+z2barsi zÎ R : zbar=z
Module :Soit z=a+ib, le module de z noté | z | = Ö (a2+b2)= Ö (z*zbar).
- |z1z2| =|z1|*|z2|si nÎ N*, |zn|=|z|nz¹ 0, |1/z| =1/|z|
- Inégalité du Triangle : |z1+z2|£ |z1|+|z2|
- 3) Interprétation Géométrique
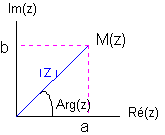
Définitions :
- z=a+ib, M un point du plan M(a,b), on appelle M(z) le point M dont d'affixe z.
- |z| est la longueur OM, |z| =OM.
- Arg(z) représente l'angle entre l'axe Ox et OM.
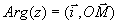
avec i le vecteur unitaire du repère (O,i,j). Arg(z) se mesure en radians.
Remarque : On voit très vite la similitude avec les vecteurs...
- L'affixe ZAB d'un vecteur AB est : ZAB=zB-zA
Propriétés :
- La distance entre points A(zA) et B(zB) est AB=|zB-zA|
- Si M(z) tel que z=a+ib et M'(z') tel que z'=zbar=a-ib, alors
OM'=OM=|z| =|zbar| et Arg(z)= - Arg(z')= - Arg(zbar) [2p ] .- Soient M1, M2, M3, M4 d'affixes z1, z2, z3, z4 ; alors on a :
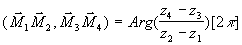
- Les vecteurs M1M2 et M3M4 sont colinéaires si et seulement si
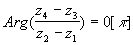
- Les vecteurs M1M2 et M3M4 sont orthogonaux si et seulement si
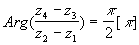
Remarques : Si Arg(z)=0[2p ]ó z Î R*+ (réel positif)
Si Arg(z)= p [2p ]ó z Î R*- (réel négatif)
Si Arg(z)= p /2[p ]ó z est un imaginaire pur.
Propriétés des Arguments :
- Arg(z1z2)=Arg(z1)+Arg(z2) d'où Arg(zn)= nArg(z)
- Arg(z1/z2)=Arg(z1)-Arg(z2) d'où Arg(1/z)= - Arg(z) car Arg(1)=0
- 4) Forme Trigonométrique et Exponentielle.
Définition : Posons q =Arg(z) et r =| z| avec z=a+ib alors on a (sachant que | z| est l'hypothénuse dans le triangle aOM (cf dessin plus haut) :
cosq =a/r et sinq =b/r et z=r (a/r +i(b/r ))óz= r [cos q +isin q ]appelée forme trigonométrique de z.
Formule de Moivre : Soit z=cosq +isinq avec | z| =1 et Arg(z)=q . D'où | zn|=1 , Arg(zn)=nq et zn=cos(nq )+isin(nq )
Donc " n Î Z (cos q +isin q )n=cos(n q )+isin(n q ) c'est la formule de Moivre.
Définition (admise): La forme exponentielle d'un complexe z= cosq +isinqest z=eiq = cos q +isin q
Les propriétés des exponentielles s'appliquent ici c'est à dire : eiqeiq'=ei(q+q')
Propriétés : si z=r (cosq +isinq ) alors z=reiqd'oùz1z2=r1r2ei(q1+q2) et z1/z2=(r1/r2)ei(q1-q2)
zbar=re-iqet 1/z=(1/r)e-iq
Passage entre les différentes formes : Soit z=a+ib, z=reiqavec z=0. On a :
a=rcosq et b=rsinq ¸r =Ö (a2+b2)¸ cosq =a/Ö (a2+b2) ¸ sinq =b/Ö (a2+b2)Formules d'Euler : On admettra les formules d'Euler :
et
.
- 5) Racines N-ièmes
Définition : Soit nÎ N* , cÎ C* et l'équation zn=c (on a donc c=a+ib), cette équation possède " n " solutions complexes zk avec 0£ kÐ n, kÎ N et |zk|= nÖ|c|(et | c| =Ö (a2+b2)). Arg(zk)=(1/n)Arg(c)+2kp /n.